Andrei Andreevich Markov (1856 – 1922) non era precisamente una persona tranquilla, aveva un carattere decisamente ruvido e poco accomodante. Nel 1874 entrò all’Università di San Pietroburgo ove studiò matematica sotto la guida del più importante matematico russo dell’epoca, il grande Pafnuty Lvovich Chebyshev (1821- 1894) che fu suo mentore e protettore. La sua carriera fu rapidissima: ancora studente nel 1877 le sue ricerche sull’uso delle frazioni continue per risolvere equazioni differenziali sono premiate con una medaglia d’oro; nel 1880 discute la tesi e nel 1884 consegue il Dottorato; a trenta anni è già professore presso l’Università di San Pietroburgo; poco dopo è eletto socio della prestigiosa Accademia delle Scienze.
Markov con il suo carattere poco conciliante ebbe non pochi problemi, da giovane venne soprannominato Andrei reistovy (il furioso), diventò poi l’accademico militante quando, da affermato scienziato, era costantemente impegnato contro l’autocrazia dello Zar, il servilismo delle istituzioni e l’oscurantismo della chiesa ortodossa. Per sua fortuna, almeno nei suoi anni giovanili, poté usufruire della protezione di Chebychev.
Ecco un elenco parziale di alcune sue attività antiautoritarie. Nel 1902 protestò contro il pavido comportamento dell’Accademia delle Scienze che, sotto pressione dello Zar, non ratificò l’elezione dello scrittore M. Gorky ed accolse come soci alcuni membri dell’aristocrazia completamente privi di meriti culturali. Quando il ministro dell’interno diede disposizioni che i docenti universitari venissero equiparati a funzionari di polizia e quindi tenuti a riferire di eventuali attività antigovernative degli studenti, Markov rispose che era un professore di teoria delle probabilità e non un poliziotto, in ogni caso non approvava queste disposizioni e non poteva cambiare opinione per ordine dei superiori.
Nel 1905 si scagliò contro le disposizioni dell’Università di San Pietroburgo sulle quote di ammissione per studenti ebrei. In seguito alla decisione del sinodo della chiesa ortodossa di scomunicare Tolstoy, Markov chiese, con una lettera formale, di essere scomunicato pure lui in quanto condivideva le posizioni del grande scrittore. La sua richiesta venne accolta, ma solo parzialmente in quanto non era stata inviata in modo appropriato; il sinodo rispose in modo formale Markov si è allontanato dalla Chiesa di Dio e noi lo espelliamo dalla lista dei Credenti Ortodossi.
Dopo la rivoluzione del 1917 il suo indiscusso prestigio scientifico e le sue opinioni progressiste contribuirono alla decisione del nuovo governo di potenziare la scuola matematica di San Pietroburgo a discapito di quella di Mosca che annoverava non pochi scienziati conservatori. Inutile dire che Andrei il furioso trovò il modo di entrare in conflitto anche con il nuovo regime.
Markov fin dalla nascita ebbe problemi alle gambe, subì diverse operazioni chirurgiche e spesso fu costretto ad usare le stampelle. Gli ultimi anni della sua vita furono rattristati dal suicidio del collega e amico Alexander Mikhailovich Lyapunov(1857-1918) e da problemi di salute; morì nel 1922 per i postumi di un’operazione alle gambe. Markov fu anche un giocatore di scacchi di livello internazionale: nel sostenne quattro partite con M. Chigorin (campione russo sfidante del campione del mondo in carica) ne vinse una pareggiando un’altra. Uno dei figli di Markov, Andrei Andreevich junior (1903-1979), ha seguito le orme del padre ed è stato un matematico di grande livello, particolarmente importanti sono i suoi contributi all’algebra ed alla logica.
L’attività di Markov, in particolare quella sul calcolo delle probabilità, si inserisce in una consolidata tradizione che risale al 1724 con la nascita dell’Accademia delle Scienze voluta da Pietro il Grande. Tra i suoi membri l’Accademia ha annoverato Eulero e Daniel Bernoulli, che nel 1738 inaugurò la probabilità in Russia con un articolo sui rischi. Da allora la probabilità è stata una delle branche preferite dai matematici russi: Chebyshev intorno al 1850, comiciò a dare piena dignità matematica alla probabilità.
Tra i contributi di Markov alla teoria della probabilità ricordiamo il perfezionamento della dimostrazione del teorema del limite centrale (TLC). La preistoria del TLC inizia nel 1738 con il risultato di De Moivre per il caso di variabili discrete con solo due valori, poi venne esteso da Laplace al caso di variabili indipendenti e discrete con varianza finita. La prima trattazione rigorosa del TLC per variabili indipendenti, non necessariamente discrete e con varianza finita è dovuta a Chebyshev, Markov e Lyapunov che utilizzarono il metodo delle funzioni caratteristiche.
Interessante è il fatto che il radicalismo di Markov non rimase un aspetto privato, ma ebbe un ruolo significativo anche nella sua attività scientifica e nella storia della teoria delle probabilità. Nel lo Zar indisse una serie di pompose celebrazioni per la ricorrenza dei 300 anni della dinastia dei Romanov, Markov, poco entusiasta dell’iniziativa, cercò di contrastare i festeggiamenti ed organizzò una grande conferenza internazionale per il secondo centenario della pubblicazione dell’Ars Conjectandi di Jacob Bernoulli ove appare la prima dimostrazione della legge dei grandi numeri.
All’inizio del 20-mo secolo Markov fu coinvolto in un animato dibattito con il matematico moscovita Nekrasov, le cui opinioni politiche e religiose erano opposte alle sue. Il controverso problema verteva sulla regolarità statistica dei comportamenti sociali. Grazie all’ attività di Quetelet, uno dei fondatori della statistica moderna, nella dominante cultura positivistica ottocentesca si era sviluppata la così detta Fisica Sociale, che interpretava le regolarità nei fenomeni sociali su grande scala come qualcosa di analogo alle leggi fisiche: Se ci diamo la pena d’esaminare e mettere insieme osservazioni accurate e sufficientemente numerose, troveremo che ciò che credevamo fosse un effetto del caso è soggetto a principi stabili …. Tutto è previsto, tutto è legge: solo la nostra ignoranza ci porta a supporre che tutto sia soggetto ai capricci del caso. Nonostante qualche riserva, ad esempio Quetelet venne da alcuni accusato di fatalismo e di tentare di applicare in modo acritico ai fenomeni sociali il determinismo di Laplace, nella seconda metà del 19-mo secolo la Fisica Sociale ebbe grande importanza in sociologia e filosofia, influenzando personaggi come Marx e Durkheim.
Nekrasov vedeva la Fisica Sociale come l’anticamera del materialismo e, peggio ancora, dell’ateismo e del marxismo e non riconosceva alle regolarità statistiche dei fenomeni sociali lo status di vere leggi, in quanto, in accordo con la tradizione della religione ortodossa, i comportamenti umani sarebbero conseguenza del libero arbitrio. Markov, al contrario, sosteneva che tali regolarità non sono altro che una conseguenza della legge dei grandi numeri.
Nekrasov fece notare che la legge dei grandi numeri non poteva essere sufficiente a spiegare la regolarità statistica, in quanto tale legge varrebbe solo sotto l’ipotesi di eventi indipendenti. L’osservazione di Nekrasov era sensata, infatti all’epoca l’unica legge dei grandi numeri dimostrata era quella di J. Bernoulli per eventi indipendenti. Markov per controbattere a questa obiezione dovette costruire una teoria di processi non indipendenti. Da una lettera ad un suo amico è ben evidente quanto fosse contento di aver messo in difficoltà il suo collega moscovita:
L’unico ruolo di P.A. Nekrasov, a mio avviso, è stato nell’aver sollevato il problema ……. Sono arrivato alla costruzione di un sistema con un carattere così generale che P.A. Nekrasov non può neanche sognarsela. Ho considerato variabili connesse in una semplice catena, da questo viene l’idea della possibilità di estendere i teoremi limite anche a queste catene.
Questo è il certificato di nascita di quei processi stocastici ora chiamati catene di Markov (CM).
Possiamo dire che le CM sono, dopo gli eventi indipendenti, il caso più semplice di processi stocastici in cui il futuro dipende (statisticamente) solo dallo stato presente e non dal passato.
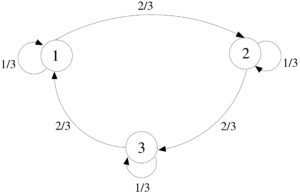
Per dare un’idea delle catene di Markov e di come sia possibile avere la legge dei grandi numeri anche per eventi non indipendenti consideriamo il seguente gioco, vedi Figura, in cui si hanno tre cerchi numerati con 1, 2 e 3; dentro ogni cerchio c’è una roulette. Un viaggiatore parte dal cerchio numero , la cui roulette è divisa in due settori, contrassegnati con il numero (in un settore di gradi) e (in un settore di gradi), il viaggiatore fa girare la roulette se esce rimane fermo, mentre se esce 2 salta nel cerchio . Abbiamo quindi che rimane in con probabilità oppure salta in con probabilità . In modo analogo il viaggiatore nello stato 2 (3) salta in 3 (1) con probabilità 2/3 e rimane in 2 (3) con probabilità 1/3. Le posizioni del viaggiatore si susseguono nel tempo e non sono indipendenti: abbiamo che da si ha più facilmente che e non si ha mai ; da si ha più facilmente che e non si può avere etc. In questo caso è semplice mostrare, usando la simmetria del problema, che la legge dei grandi numeri vale: nonostante gli eventi non siano indipendenti, se il gioco viene protratto a lungo il viaggiatore passa in ogni cerchio un terzo del tempo.
Originariamente Markov considerò il caso con variabili dicotomiche, in seguito trattò il caso più generale con un numero finito di stati, dimostrando come la legge dei grandi numeri valga, sotto opportune condizioni sulle probabilità di salto tra gli stati. Pochi anni dopo Markov utilizzò le CM per un’analisi statistica di alcuni testi di Pushkin; il suo approccio era piuttosto rudimentale in quanto trattava il testo come una successione di vocali e consonanti, tuttavia questi lavori sono stati il punto di partenza dell’uso di tecniche probabilistiche per la linguistica: oggi le CM sono usate per l’attribuzione dei testi.
Le catene di Markov che descrivono sistemi che assumono solo stati discreti ed evolvono con un tempo discreto, costituiscono il caso più semplice non banale di processo stocastico. Lo sviluppo di questo campo ha avuto forti impulsi e motivazioni dalla fisica, in particolare dallo studio del moto browniano all’inizio del 20-mo secolo da parte di Einstein, Smoluchowski e Langevin. Negli anni 30 Kolmogorov ha iniziato la formalizzazione dei processi stocastici markoviani: oltre alle CM con un numero finito di stati, anche le CM con un numero infinito numerabile di stati, ed inoltre i processi con stati discreti e tempo continuo (descritti dalle così dette master equations) e quelli con stati continui e tempo continuo (regolati dalle equazioni di Fokker- Planck). Ora i processi stocastici trovano applicazioni nei campi più svariati: in fisica, chimica, biologia nonché in economia e finanza.
Magari si potrebbe pensare che le CM siano astrusi strumenti matematici che riguardano solo gli scienziati, in realtà le incontriamo, senza saperlo, tutti i giorni: ogni volta che usiamo Google (od altri motori di ricerca su Internet) stiamo utilizzando le catene di Markov. Quando si inseriscono delle parole su Google (ad esempio Markov chains applications) il motore di ricerca, con un metodo basato sulle catene di Markov, usando un algoritmo personalizzato diverso da utente ad utente che privilegia le pagine ed i siti visitati in passato, fornisce un elenco, in ordine di importanza, delle pagine che contengono le parole desiderate.
Angelo Vulpiani
Dipartimento di Fisica, Università, Sapienza di Roma
Qualche lettura per approfondire:
- G.P. Basharin, A.N. Langville and V.A. Naumov ”The life and work of A.A. Markov” Linear Algebra and its Applications 386, 3 (2004).
- L. Graham and J-M. Kantor Naming infinity: a true story of religious mysticism and mathematical creativity (Belknap Press, 2009).
- B. Hayes ”First Links in the Markov Chain” American Scientist 101, 92 (2013).
- D.V. Khmelev and F.J. Tweedie ”Using Markov chains for identification of writers” Literary an Linguistic Computing 16, 299 (2001).
- E. Seneta ”Markov and the Birth of Chain Dependence Theory” International Statistical Review 64, 255 (1966).
- E. Seneta ”Statistical regularity and free will: L.A.J. Quetelet and P.A. Nekrasov” International Statistical Review 71, 319 (2003).
- A. Vulpiani “Caso, proabilità e complessità” (Ediesse, 2014).
- A. Vulpiani ”Andrei Andreevich Markov: un matematico furioso e le sue catene”, Lettera Matematica 94, 6 (2015).